
목표
TensorFlow Keras library 를 사용해서 CIFAR-10 dataset 같은 이미지를 생성하는 간단한 diffusion 모델을 만들어볼 것이다.
다음은 diffusion 모델이 동작하는 방식이고, fully noised 이미지에서부터 점진적으로 이미지를 생성해나간다.

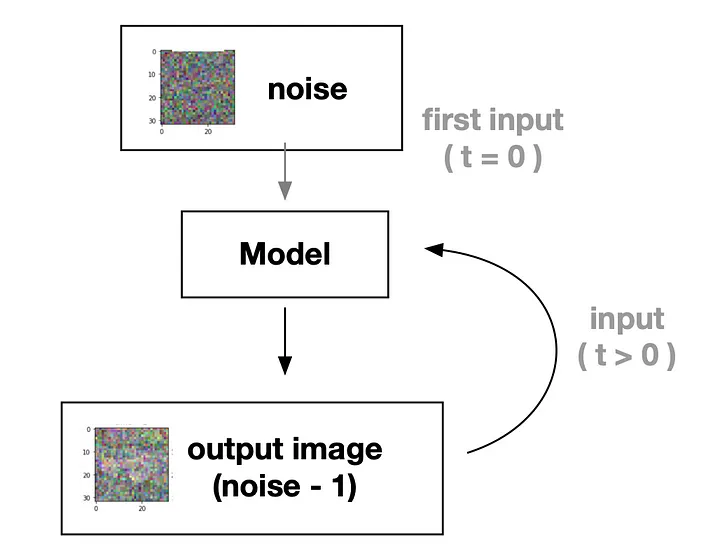

위에서 봤듯이, 이 모델은 점진적으로 노이즈를 줄여가면서 이미지를 생성한다. 따라서 본 딥러닝 모델에게 noise 를 줄이는 방법을 학습시킬 것이며 이를 위해 두가지 입력이 필요하다.
- 입력 : 처리되어야할 초기 Noise
- timestamp : noise status
Importing necessary libraries
import numpy as np
from tqdm.auto import trange, tqdm
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras import layers
Prepare the dataset
CIFAR-10 데이터 셋으로부터 학습 데이터를 불러온다.
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.cifar10.load_data()
X_train = X_train[y_train.squeeze() == 1]
X_train = (X_train / 127.5) - 1.0
Define variables
IMG_SIZE = 32 # input image size, CIFAR-10 is 32x32
BATCH_SIZE = 128
timesteps = 16 # how many steps for a noisy image into clear
time_bar = 1 - np.linspace(0, 1.0, timesteps + 1) # linspace for timesteps
time_bar는 확산 모델(Diffusion Model)에서 사용되는 시간 스케일링(time scaling)에 관련된 값이다.
이 과정에서 사용되는 핵심 개념 중 하나가 노이즈의 스케일을 시간에 따라 조절하는 것인데,
time_bar는 0에서 1까지의 값을 가지는 벡터로, 해당 값은 노이즈 스케일을 나타낸다. 보통 0에서 1로 변하는 time_bar는 각 단계에서의 노이즈의 강도를 조정하는 데 사용된다. time_bar[0]은 초기 단계에서의 노이즈 강도를 나타내고, time_bar[timesteps]는 마지막 단계에서의 노이즈 강도를 나타낸다. 노이즈의 강도가 점차적으로 감소하도록 설계되어 있어, 초기 단계에서는 높은 노이즈가 추가되고 나중에는 저레벨의 노이즈만 남게 된다.
Some utility functions for preview data
이미지 데이터를 정규화하고 시각화하는 함수들을 포함한다.
def cvtImg(img):
img = img - img.min() # Subtract the minimum value of the image array to make it zero-centered.
img = (img / img.max()) # Normalize the image to be between 0 and 1.
return img.astype(np.float32) # Return the normalized image as float32 type.
def show_examples(x):
plt.figure(figsize=(10, 10)) # Create a new plot window of size 10x10 inches.
for i in range(25): # Generate 25 subplots and plot each image on each subplot.
plt.subplot(5, 5, i+1)
img = cvtImg(x[i]) # Normalize the image using the cvtImg function.
plt.imshow(img) # Plot the normalized image.
plt.axis('off') # Remove axes to display the image cleanly.
show_examples(X_train)
1. cvtImg(img) 함수 : 이미지를 정규화한다.
2. show_examples(X_train) : X_train에 있는 처음 25개의 이미지를 정규화하고 시각적으로 표시
이 때, 하나의 플롯은 일반적으로 하나의 도표를 말하며 서브 플롯이란
하나의 플롯 영역 내에서 여러 개의 작은 도표를 배열 형태로 배치하는 것을 말한다.
Forward process
def forward_noise(x, t):
a = time_bar[t] # base on t
b = time_bar[t + 1] # image for t + 1
# Make a Gaussian noise to be applied on x
noise = np.random.randn(*x.shape)
a = a.reshape((-1, 1, 1, 1))
b = b.reshape((-1, 1, 1, 1))
img_a = x * (1 - a) + noise * a # computes the image at time t
img_b = x * (1 - b) + noise * b # computes the image at time t + 1
return img_a, img_b
def generate_ts(num):
return np.random.randint(0, timesteps, size=num)
t = generate_ts(25) # random for training data
a, b = forward_noise(X_train[:25], t)
show_examples(a)
- a,b : 각각 시간 t와 t + 1에서 추가할 노이즈의 양을 결정
- random.randn() : 평균이 0이고 표준편차가 1인 정규 분포(가우시안 분포)를 따르는 난수를 생성. *을 사용하는 이유는 x.shape의 튜플을 unpack하여 np.random.randn 함수에 전달하기 위함이다. 예를 들어 x.shape가 (32, 32, 3) 인 경우, *x.shape는 32, 32, 3으로 풀린다. np.random.randn(*x.shape)는 np.random.randn(32, 32, 3)과 같이 호출되는 역할을 한다.


Q. 스칼라 값인 a,b 를 reshape((-1, 1, 1, 1))하는 이유?
A. a가 스칼라이기 때문에 추가적인 차원을 부여하더라도 실제로는 형태에 큰 변화가 없지만, 코드의 일관성을 유지하고 다차원 배열을 다루기 쉽게 하는 데 도움이 된다. 인풋 데이터인 x 와의 연산을 편리하게 수행할 수 있다.
Building a block
각각의 블럭은 Time Parameter 와 함께 두개의 convolutional networks를 포함하며, 이것은 information에 따라 현재 time step 과 결과를 결정할 수 있도록 한다. 아래와 같은 플로우 차트 이미지를 확인할 수 있고, x_img 는 noizy 한 input image 이고 x_ts 는 time step 별 입력이다. 즉, 본 block 은 입력 이미지 (x_img)에서 CNN을 사용하여 특징을 추출하고, 이를 시간적인 파라미터 (x_ts)와 결합하여 최종적인 출력 (x_out)을 생성하는 역할을 한다. 이러한 과정을 통해 diffusion 모델은 이미지의 특징을 시간적인 요소와 함께 고려하여 처리할 수 있게 된다.

- Conv2D: 128 channels, 3x3 conv, padding same, ReLU activation (input: x_img, output: x_parameter)
- Time Parameter: dense layer with 128 hidden units (input: x_ts, output: time_parameter)
def block(x_img, x_ts):
x_parameter = layers.Conv2D(128, (3, 3), padding='same', activation='relu')(x_img)
x_out = layers.Conv2D(128, (3, 3), padding='same', activation='relu')(x_img)
# Time parameter
time_parameter = layers.Dense(128)(x_ts)
# New x_parameter
x_parameter = layers.Multiply()([x_parameter, time_parameter])
# New x_out
x_out = layers.Add()([x_out, x_parameter])
x_out = layers.LayerNormalization()(x_out)
x_out = layers.Activation('relu')(x_out)
return x_out
Building an U-Net
Diffusion 모델은 이미지를 생성하는 과정에서 원본 이미지의 구조를 보존하고, 객체의 일부분을 변형하거나 추가할 수 있어야 한다.
이를 위해 U-Net은 객체를 정확하게 분할하여 각 객체의 경계를 명확히 구분할 수 있다. 이미지 생성 과정에서 객체의 정확한 인식과 배치를 보장하며, 최종적으로 높은 품질의 생성 이미지를 생성하는 데 기여한다.
U-Net 이란?
이미지 분석에서 사용되는 딥러닝 아키텍처로, 이미지 세그멘테이션(이미지 내의 특정 객체를 픽셀 수준에서 식별 및 분할하는 작업)에 특화된 네트워크이다. 인코더-디코더(Encoder-Decoder) 구조를 기반으로 하며, 특히 Fully Convolutional Network (FCN)의 변형으로 볼 수 있다. 인코더 부분에서는 이미지의 공간적인 정보를 단계적으로 축소해가며 추출하고, 디코더 부분에서는 이를 업샘플링하여 원본 이미지의 크기로 복원하면서 세그멘테이션을 수행한다.
1) Contracting Path (인코더) : 입력 이미지를 점점 줄여가며 특징을 추출하는 단계이다. 주로 Convolutional layer와 Pooling layer를 사용하여 이미지의 공간적인 해상도를 축소한다.
2) Expanding Path (디코더) : Contracting Path에서 얻은 특징을 바탕으로 입력 이미지의 크기로 업샘플링하면서 세그멘테이션 맵을 생성한다.
3) Skip Connections : 인코더의 각 단계에서 해당 스텝의 출력을 디코더에 연결하여 세밀한 특징 정보가 세그멘테이션 결과에 반영되도록 돕는다. 이는 네트워크가 정확한 위치에 대한 세그멘테이션을 수행할 수 있게 한다.
4) Final Layer : 디코더의 마지막 층에서는 세그멘테이션 클래스 수에 맞는 출력을 생성한다. 일반적으로는 각 픽셀이 해당 클래스에 속할 확률을 나타내는 softmax activation function을 사용한다.

def make_model():
x = x_input = layers.Input(shape=(IMG_SIZE, IMG_SIZE, 3), name='x_input')
x_ts = x_ts_input = layers.Input(shape=(1,), name='x_ts_input')
x_ts = layers.Dense(192)(x_ts)
x_ts = layers.LayerNormalization()(x_ts)
x_ts = layers.Activation('relu')(x_ts)
# ----- left ( down ) -----
x = x32 = block(x, x_ts)
x = layers.MaxPool2D(2)(x)
x = x16 = block(x, x_ts)
x = layers.MaxPool2D(2)(x)
x = x8 = block(x, x_ts)
x = layers.MaxPool2D(2)(x)
x = x4 = block(x, x_ts)
# ----- MLP -----
x = layers.Flatten()(x)
x = layers.Concatenate()([x, x_ts])
x = layers.Dense(128)(x)
x = layers.LayerNormalization()(x)
x = layers.Activation('relu')(x)
x = layers.Dense(4 * 4 * 32)(x)
x = layers.LayerNormalization()(x)
x = layers.Activation('relu')(x)
x = layers.Reshape((4, 4, 32))(x)
# ----- right ( up ) -----
x = layers.Concatenate()([x, x4])
x = block(x, x_ts)
x = layers.UpSampling2D(2)(x)
x = layers.Concatenate()([x, x8])
x = block(x, x_ts)
x = layers.UpSampling2D(2)(x)
x = layers.Concatenate()([x, x16])
x = block(x, x_ts)
x = layers.UpSampling2D(2)(x)
x = layers.Concatenate()([x, x32])
x = block(x, x_ts)
# ----- output -----
x = layers.Conv2D(3, kernel_size=1, padding='same')(x)
model = tf.keras.models.Model([x_input, x_ts_input], x)
return model
model = make_model()
- tf.keras.models.Model([x_input, x_ts_input], x) : 입력으로 x_input 과 x_ts_input 두개의 입력을 받고, 출력으로 x를 반환하는 모델을 정의한다.
def mse_loss(y_true, y_pred):
return tf.reduce_mean(tf.square(y_true - y_pred))optimizer = tf.keras.optimizers.Adam(learning_rate=0.0008)
loss_func = mse_loss
model.compile(loss=loss_func, optimizer=optimizer)
일반적으로 이미지 생성 작업에 적합한 손실 함수로는 평균 제곱 오차(Mean Squared Error, MSE) 로서,
생성된 이미지와 목표 이미지 사이의 픽셀별 차이의 제곱을 평균하여 계산한다. 이때, 훈련 과정에서 y_true와 y_pred가 손실함수로 자동으로 전달된다.

Predict the result
노이즈 이미지로부터 실제 이미지를 생성하는 과정을 나타내고 있다.
def predict(x_idx=None):
x = np.random.normal(size=(32, IMG_SIZE, IMG_SIZE, 3))
for i in trange(timesteps):
t = i
x = model.predict([x, np.full((32), t)], verbose=0)
show_examples(x)
predict()
- 모델에 입력될 초기 입력 이미지 x를 정규 분포를 따르는 난수로 생성한다.
- timesteps 은 예측하는 동안 진행할 시간 단계이다.
- 모델을 사용하여 입력 이미지 x와 현재 시간 t를 이용해 다음 시간 단계의 이미지를 예측한다.
- 이 때, np.full((32), t) 는 크기가 32이고 모든 요소가 t로 채워진 배열이다. 모든 배치 샘플에 동일한 시간 단계 t를 적용하기 위해 사용된다.
- 결론적으로 초기 랜덤이미지에서 t번 노이즈를 제거한 결과가 출력된다.
Split the dataset into train and test sets
이미지 생성 과정에서 예측 스텝을 수행하고, 매 두 번째 시간 단계마다 생성된 이미지를 시각화하는 함수이다.
def predict_step():
xs = []
x = np.random.normal(size=(8, IMG_SIZE, IMG_SIZE, 3))
for i in trange(timesteps):
t = i
x = model.predict([x, np.full((8), t)], verbose=0)
if i % 2 == 0:
xs.append(x[0])
plt.figure(figsize=(20, 2))
for i in range(len(xs)):
plt.subplot(1, len(xs), i+1)
plt.imshow(cvtImg(xs[i]))
plt.title(f'{i}')
plt.axis('off')
predict_step()
Training model
def train_one(x_img):
t = generate_ts(BATCH_SIZE) # Generate random timesteps for the batch
x_a, x_b = forward_noise(x_img, t) # Generate noisy images
x_ts = np.array(t).reshape(-1, 1) # Reshape timesteps for model input
loss = model.train_on_batch([x_a, x_ts], x_b) # single gradient update on a single batch of data
return loss
- 모델을 한 배치(batch)만큼 학습시키고 그 손실 값을 반환하는 함수이다.
- 이를 위해서 forward_noise 함수로부터 노이즈가 추가된 이미지를 생성하고, 해당 이미지와 타임스텝을 입력으로 하여 모델을 학습시킨다.
- 즉 모델은 Xt 시점의 이미지 x_a 를 가지고 노이즈를 추가하여 Xt+1 시점의 이미지를 예측하며, 실제 Xt+1 이미지의 ground truth 인 x_b 와의 비교를 통해 최종 손실을 구해내게 된다.
Model.train_on_batch( x, y=None, sample_weight=None, class_weight=None, return_dict=False )
def train(R=50):
bar = trange(R)
total = 100
for i in bar:
for j in range(total):
# X_train 배열에서 임의의 인덱스를 선택하여 BATCH_SIZE 만큼의 이미지 데이터를 가져옴
x_img = X_train[np.random.randint(len(X_train), size=BATCH_SIZE)]
loss = train_one(x_img)
pg = (j / total) * 100
if j % 5 == 0:
bar.set_description(f'loss: {loss:.5f}, p: {pg:.2f}%')
- train() 함수는 한번의 에포크를 실행.
- trange(R) : 진행 상황을 표시하는 진행 막대를 생성
- 각 에포크마다 total 번의 반복을 수행. 훈련 데이터를 여러 배치로 나누어 처리하는 과정을 의미.
- train_one 함수를 호출하여 현재 배치의 입력 이미지 x_img를 사용하여 모델을 훈련하고 손실값을 반환받음
for _ in range(10):
train()
model.optimizer.learning_rate = max(0.000001, model.optimizer.learning_rate * 0.9)
predict()
predict_step()
plt.show()결과


Ref
https://www.tensorflow.org/tutorials/generative/generate_images_with_stable_diffusion
'CS > 인공지능' 카테고리의 다른 글
| SVM 을 활용한 스팸 분류기 ( Spam Classification via SVM ) (1) | 2024.10.17 |
|---|---|
| 나이브 베이즈를 사용한 스팸 메일 분류기 (Spam Classification via Naïve Bayes) (3) | 2024.10.17 |
| Simple Diffusion Image generate Model (0) | 2024.06.21 |
| [TensorFlow Keras] 손글씨 이미지를 생성하는 GAN model 만들기 (0) | 2024.05.29 |
| Generative Adversarial Network (1) | 2024.05.28 |



